Adding a patient callback from a nurse#
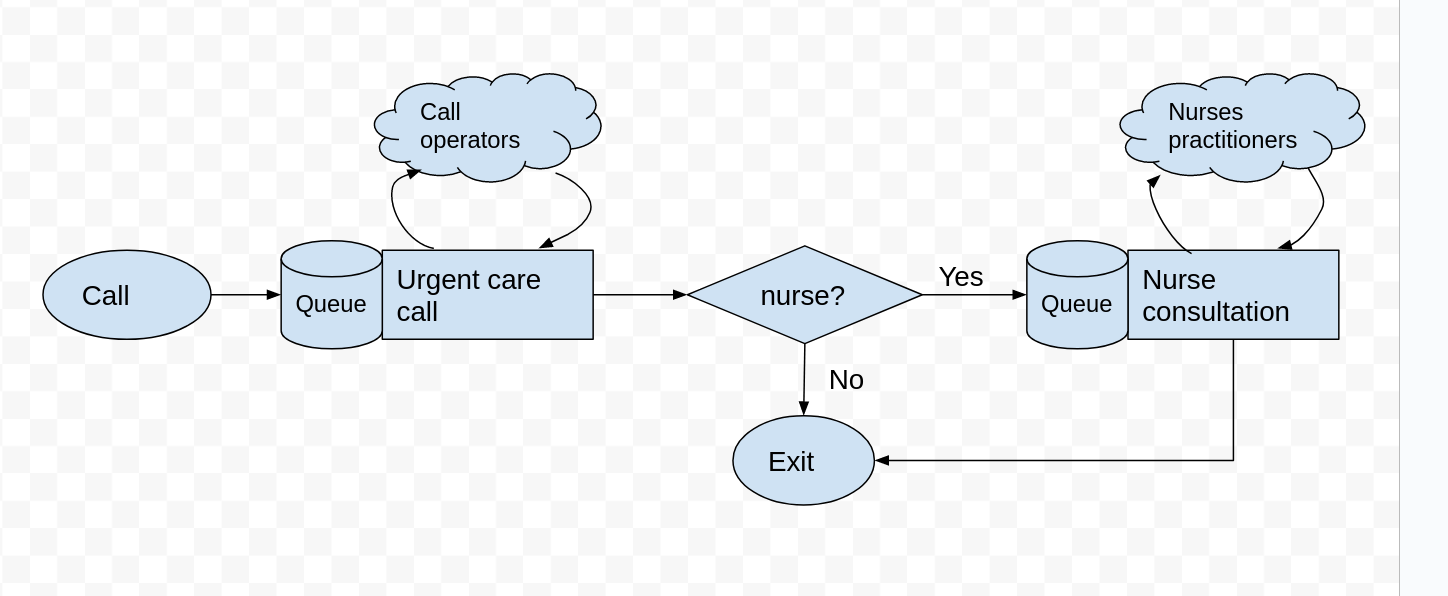
After a patient has spoken to a call operator their priority is triaged. It is estimated that 40% of patients require a callback from a nurse. There are 9 nurses available. A nurse patient consultation has a Uniform distribution lasting between 10 and 20 minutes.
Task
Add a new decision variable to
Experimentcalln_nurses.Create a second
simpy.Resourcecallednursesand add it to the simulation model.Modify the logic of
serviceso that 40% of patients are called back.Collect results and estimate the waiting time for a nurse callback and a nurse utilisation.
Hints
Use the classes added called Uniform and Bernoulli distribution classes.
Not all patients will see a nurse - use the Bernoulli distribution to sample a True or False value.
The logic for taking a nurse resource and then undergoing a nurse consultation is the same the operator process.
1. Imports#
import numpy as np
import pandas as pd
import simpy
import itertools
2. Notebook level variables, constants, and default values#
A useful first step when setting up a simulation model is to define the base case or as-is parameters. Here we will create a set of constant/default values for our Experiment class, but you could also consider reading these in from a file.
# default resources
N_OPERATORS = 13
# ##############################################################################
# MODIFICATION: number of nurses available
# your code here...
################################################################################
# default mean inter-arrival time (exp)
MEAN_IAT = 60 / 100
## default service time parameters (triangular)
CALL_LOW = 5.0
CALL_MODE = 7.0
CALL_HIGH = 10.0
# ##############################################################################
# MODIFICATION: nurse distribution parameters
# your code here ...
################################################################################
# Seeds for arrival and service time distributions (for repeatable single run)
ARRIVAL_SEED = 42
CALL_SEED = 101
# ##############################################################################
# MODIFICATION: additional seeds for new activities
# your code here ...
# ##############################################################################
# Boolean switch to simulation results as the model runs
TRACE = False
# run variables
RESULTS_COLLECTION_PERIOD = 1000
3. Distribution classes#
We will define two additional distribution classes (Uniform and Bernoulli) to encapsulate the random number generation, parameters and random seeds used in the sampling. Take a look at how they work.
You should be able to reuse these classes in your own simulation models. It is actually not a lot of code, but it is useful to build up a code base that you can reuse with confidence in your own projects.
class Bernoulli():
'''
Convenience class for the Bernoulli distribution.
packages up distribution parameters, seed and random generator.
Use the Bernoulli distribution to sample success or failure.
'''
def __init__(self, p, random_seed=None):
'''
Constructor
Params:
------
p: float
probability of drawing a 1
random_seed: int, optional (default=None)
A random seed to reproduce samples. If set to none then a unique
sample is created.
'''
self.rand = np.random.default_rng(seed=random_seed)
self.p = p
def sample(self, size=None):
'''
Generate a sample from the exponential distribution
Params:
-------
size: int, optional (default=None)
the number of samples to return. If size=None then a single
sample is returned.
Returns:
-------
float or np.ndarray (if size >=1)
'''
return self.rand.binomial(n=1, p=self.p, size=size)
class Uniform():
'''
Convenience class for the Uniform distribution.
packages up distribution parameters, seed and random generator.
'''
def __init__(self, low, high, random_seed=None):
'''
Constructor
Params:
------
low: float
lower range of the uniform
high: float
upper range of the uniform
random_seed: int, optional (default=None)
A random seed to reproduce samples. If set to none then a unique
sample is created.
'''
self.rand = np.random.default_rng(seed=random_seed)
self.low = low
self.high = high
def sample(self, size=None):
'''
Generate a sample from the exponential distribution
Params:
-------
size: int, optional (default=None)
the number of samples to return. If size=None then a single
sample is returned.
Returns:
-------
float or np.ndarray (if size >=1)
'''
return self.rand.uniform(low=self.low, high=self.high, size=size)
class Triangular():
'''
Convenience class for the triangular distribution.
packages up distribution parameters, seed and random generator.
'''
def __init__(self, low, mode, high, random_seed=None):
'''
Constructor. Accepts and stores parameters of the triangular dist
and a random seed.
Params:
------
low: float
The smallest values that can be sampled
mode: float
The most frequently sample value
high: float
The highest value that can be sampled
random_seed: int, optional (default=None)
Used with params to create a series of repeatable samples.
'''
self.rand = np.random.default_rng(seed=random_seed)
self.low = low
self.high = high
self.mode = mode
def sample(self, size=None):
'''
Generate one or more samples from the triangular distribution
Params:
--------
size: int
the number of samples to return. If size=None then a single
sample is returned.
Returns:
-------
float or np.ndarray (if size >=1)
'''
return self.rand.triangular(self.low, self.mode, self.high, size=size)
class Exponential():
'''
Convenience class for the exponential distribution.
packages up distribution parameters, seed and random generator.
'''
def __init__(self, mean, random_seed=None):
'''
Constructor
Params:
------
mean: float
The mean of the exponential distribution
random_seed: int, optional (default=None)
A random seed to reproduce samples. If set to none then a unique
sample is created.
'''
self.rand = np.random.default_rng(seed=random_seed)
self.mean = mean
def sample(self, size=None):
'''
Generate a sample from the exponential distribution
Params:
-------
size: int, optional (default=None)
the number of samples to return. If size=None then a single
sample is returned.
Returns:
-------
float or np.ndarray (if size >=1)
'''
return self.rand.exponential(self.mean, size=size)
3. Experiment class#
We will modify the experiment class to include new results collection for the additional nurse process.
Modify the init method to accept additional parameters:
n_nurses,chance_callback,nurse_call_low,nurse_call_high,callback_seed,nurse_seed. Remember to include the default values for these parameters.Store parameters in the class and create new distributions.
Add variables to support KPI calculation to the
resultsdictionary fornurse_waiting_timesandtotal_nurse_call_duration
class Experiment:
'''
Parameter class for 111 simulation model
'''
# ##########################################################################
# MODIFICATION: update the __init__ method to accept new parameters
# for the n_nurses, chance_callback, nurse_call_low, nurse_call_high,
# callback_seed, nurse_seed.
# remember to include the default values for these parameters.
def __init__(self, n_operators=N_OPERATORS,
mean_iat=MEAN_IAT, call_low=CALL_LOW, call_mode=CALL_MODE,
call_high=CALL_HIGH, arrival_seed=None, call_seed=None):
'''
The init method sets up our defaults.
'''
self.n_operators = n_operators
# ######################################################################
# MODIFICATION: store the number of nurses in the experiment
# your code here ...
# ######################################################################
self.arrival_dist = Exponential(mean_iat, random_seed=arrival_seed)
self.call_dist = Triangular(call_low, call_mode, call_high,
random_seed=call_seed)
# ######################################################################
# MODIFICATION create the callback and nurse consultation distributions
# your code here ...
# ######################################################################
# resources: we must init resources inside of the arrivals process.
# but we will store a placeholder for them for transparency
self.operators = None
# ######################################################################
# MODIFICATION: nurse resource placeholder.
# your code here ...
# ######################################################################
# initialise results to zero
self.init_results_variables()
def init_results_variables(self):
'''
Initialise all of the experiment variables used in results
collection. This method is called at the start of each run
of the model
'''
# variable used to store results of experiment
self.results = {}
self.results['waiting_times'] = []
# total operator usage time for utilisation calculation.
self.results['total_call_duration'] = 0.0
# ######################################################################
# MODIFICATION: nurse sub process results collection
# your code here ...
# ######################################################################
4. Model code#
def trace(msg):
'''
Turing printing of events on and off.
Params:
-------
msg: str
string to print to screen.
'''
if TRACE:
print(msg)
def service(identifier, args, env):
'''
simulates the service process for a call operator
1. request and wait for a call operator
2. phone triage (triangular)
3. exit system
Params:
------
identifier: int
A unique identifer for this caller
experiment: Experiment
The settings and input parameters for the current experiment
env: simpy.Environment
The current environent the simulation is running in
We use this to pause and restart the process after a delay.
'''
# record the time that call entered the queue
start_wait = env.now
# request an operator
with args.operators.request() as req:
yield req
# record the waiting time for call to be answered
waiting_time = env.now - start_wait
# store the results for an experiment
args.results['waiting_times'].append(waiting_time)
trace(f'operator answered call {identifier} at ' \
+ f'{env.now:.3f}')
# the sample distribution is defined by the experiment.
call_duration = args.call_dist.sample()
# schedule process to begin again after call_duration
yield env.timeout(call_duration)
# update the total call_duration
args.results['total_call_duration'] += call_duration
# print out information for patient.
trace(f'call {identifier} ended {env.now:.3f}; ' \
+ f'waiting time was {waiting_time:.3f}')
# ############################################################
# MODIFICATION: NURSE CALL BACK
# 1. does nurse need to call back?
# 2. request nurse resource (and wait_
# 3. undergo nurse consultation (delay)
# 4. track how long patient waited and nurse utilisation
# your code here ...
def arrivals_generator(env, args):
'''
IAT is exponentially distributed
Parameters:
------
env: simpy.Environment
The simpy environment for the simulation
experiment: Experiment
The settings and input parameters for the simulation.
'''
# use itertools as it provides an infinite loop
# with a counter variable that we can use for unique Ids
for caller_count in itertools.count(start=1):
# the sample distribution is defined by the experiment.
inter_arrival_time = args.arrival_dist.sample()
yield env.timeout(inter_arrival_time)
trace(f'call arrives at: {env.now:.3f}')
# we pass the experiment to the service function
env.process(service(caller_count, args, env))
5. Model wrapper functions#
Modifications to make to the single_run function:
Create and the nurses resource to the experiment
After the simulation is complete calculate the mean waiting time and mean nurse utilisation.
Hints:
To create a nurse resource and assign it to the experiment you can use the following code:
experiment.nurses = simpy.Resource(env, capacity=experiment.n_nurses)
You can copy and adapt the results code from call operators to nurses.
You do not need to make any modifications to the
multiple_replicationsfunction
def single_run(experiment, rc_period=RESULTS_COLLECTION_PERIOD):
'''
Perform a single run of the model and return the results
Parameters:
-----------
experiment: Experiment
The experiment/paramaters to use with model
'''
# results dictionary. Each KPI is a new entry.
run_results = {}
# reset all results variables to zero and empty
experiment.init_results_variables()
# environment is (re)created inside single run
env = simpy.Environment()
# we create simpy resource here - this has to be after we
# create the environment object.
experiment.operators = simpy.Resource(env, capacity=experiment.n_operators)
# #########################################################################
# MODIFICATION: create the nurses resource
# your code here ...
# #########################################################################
# we pass the experiment to the arrivals generator
env.process(arrivals_generator(env, experiment))
env.run(until=rc_period)
# end of run results: calculate mean waiting time
run_results['01_mean_waiting_time'] = \
np.mean(experiment.results['waiting_times'])
# end of run results: calculate mean operator utilisation
run_results['02_operator_util'] = \
(experiment.results['total_call_duration'] \
/ (rc_period * experiment.n_operators)) * 100.0
# #########################################################################
# MODIFICATION: summary results for nurse process
# end of run results: nurse waiting time
# your code here...
# end of run results: calculate mean nurse utilisation
# your code here...
# #########################################################################
# return the results from the run of the model
return run_results
def multiple_replications(experiment,
rc_period=RESULTS_COLLECTION_PERIOD,
n_reps=5):
'''
Perform multiple replications of the model.
Params:
------
experiment: Experiment
The experiment/paramaters to use with model
rc_period: float, optional (default=DEFAULT_RESULTS_COLLECTION_PERIOD)
results collection period.
the number of minutes to run the model to collect results
n_reps: int, optional (default=5)
Number of independent replications to run.
Returns:
--------
pandas.DataFrame
'''
# loop over single run to generate results dicts in a python list.
results = [single_run(experiment, rc_period) for rep in range(n_reps)]
# format and return results in a dataframe
df_results = pd.DataFrame(results)
df_results.index = np.arange(1, len(df_results)+1)
df_results.index.name = 'rep'
return df_results
TRACE = False
default_scenario = Experiment()
results = multiple_replications(default_scenario)
results
| 01_mean_waiting_time | 02_operator_util | |
|---|---|---|
| rep | ||
| 1 | 3.152600 | 93.604316 |
| 2 | 7.141390 | 96.434407 |
| 3 | 1.627092 | 89.803993 |
| 4 | 1.374022 | 89.258187 |
| 5 | 4.852374 | 90.147745 |
6. Multiple experiments#
No modifications are needed to code in this section.
The single_run and multiple_replications wrapper functions for the model and the Experiment class mean that is very simple to run multiple experiments using replication analysis. We will define three new functions for running multiple experiments:
get_experiments()- this will return a python dictionary containing a unique name for an experiment paired with anExperimentobjectrun_all_experiments()- this will loop through the dictionary, run all experiments and return combined results.experiment_summary_frame()- take the results from each scenario and format into a simple table.
def get_experiments():
'''
Creates a dictionary object containing
objects of type `Experiment` to run.
Returns:
--------
dict
Contains the experiments for the model
'''
experiments = {}
# base case
experiments['base'] = Experiment()
# +1 extra capacity
experiments['operators+1'] = Experiment(n_operators=N_OPERATORS+1)
return experiments
def run_all_experiments(experiments, rc_period=RESULTS_COLLECTION_PERIOD):
'''
Run each of the scenarios for a specified results
collection period and replications.
Params:
------
experiments: dict
dictionary of Experiment objects
rc_period: float
model run length
'''
print('Model experiments:')
print(f'No. experiments to execute = {len(experiments)}\n')
experiment_results = {}
for exp_name, experiment in experiments.items():
print(f'Running {exp_name}', end=' => ')
results = multiple_replications(experiment, rc_period)
print('done.\n')
#save the results
experiment_results[exp_name] = results
print('All experiments are complete.')
# format thje results
return experiment_results
# get the experiments
experiments = get_experiments()
#run the scenario analysis
experiment_results = run_all_experiments(experiments)
Model experiments:
No. experiments to execute = 2
Running base => done.
Running operators+1 => done.
All experiments are complete.
def experiment_summary_frame(experiment_results):
'''
Mean results for each performance measure by experiment
Parameters:
----------
experiment_results: dict
dictionary of replications.
Key identifies the performance measure
Returns:
-------
pd.DataFrame
'''
columns = []
summary = pd.DataFrame()
for sc_name, replications in experiment_results.items():
summary = pd.concat([summary, replications.mean()], axis=1)
columns.append(sc_name)
summary.columns = columns
return summary
# as well as rounding you may want to rename the cols/rows to
# more readable alternatives.
summary_frame = experiment_summary_frame(experiment_results)
summary_frame.round(2)
| base | operators+1 | |
|---|---|---|
| 01_mean_waiting_time | 4.32 | 0.95 |
| 02_operator_util | 93.97 | 85.67 |


